Lentilles minces et convergentes
Ondes et signaux
Ajouter à mes favoris
Notions
Relation de conjugaison d’une lentille mince convergente.
Grandissement.Image réelle, image virtuelle, image droite, image renversée.
Compétences attendues
Exploiter les relations de conjugaison et de grandissement fournies pour déterminer la position et la taille de l’image d’un objet-plan réel.
Déterminer les caractéristiques de l’image d’un objet-plan réel formée par une lentille mince convergente.
Estimer la distance focale d’une lentille mince convergente.
Tester la relation de conjugaison d’une lentille mince convergente.
Réaliser une mise au point en modifiant soit la distance focale de la lentille convergente soit la géométrie du montage optique.
Capacités mathématiques : Utiliser le théorème de Thalès. Utiliser des grandeurs algébriques.
Introduction
Qu’est-ce qu’une lentille ?
Une lentille est constituée d’un milieu transparent ( verre, matière plastique, eau etc ) limité par deux faces dont l’une au moins est sphérique. ( on peut avoir deux faces sphériques ou une face sphérique et l’autre plane.
Points particuliers et grandeurs caractéristiques
Axe optique
L’axe optique d’une lentille est aussi appelé axe de symétrie du système. Il passe par le centre de la lentille que l’on appelle le centre optique et est perpendiculaire au plan de la lentille.

Centre optique
Le centre optique est le milieu d’une lentille, on le note O. Lorsqu’on représente une lentille, on aligne son centre optique sur l’axe optique.

Foyer image
Le foyer image est le point de l’axe optique vers lequel converge un faisceau lumineux incident parallèle à l’axe optique. On le note F’.

Foyer objet
Le foyer objet est le point duquel partent les rayons lumineux qui émergent de la lentille parallèlement à l’axe optique. Le foyer objet est le symétrique du point F’ par rapport au centre optique. On le note F.

Types de lentilles
Les relations de conjugaison et de grandissement
Position et taille de l’image
La position de l’image d’un objet est obtenue en utilisant les trois rayons caractéristiques :
Les rayons qui passent par le centre optique ne sont pas déviés.
Les rayons qui arrivent parallèles à l’axe optique émergent en passant par le foyer image F’.
Les rayons qui passent par le foyer objet F émergent parallèles à l’axe optique.
Activité - Tracer les rayons lumineux
L’image d’un point se forme à l’intersection des rayons lumineux provenant de ce point.
Activité - Construire une image
Il est possible, par le calcul, de prévoir le résultat issu de cette construction géométrique. Pour cela, on choisit un repère dont l’origine est le centre optique O de la lentille. L’axe optique Δ, est l’axe des abscisses x. L’axe perpendiculaire à l’axe optique Δ, passant par le centre optique de la lentille, est l’axe des ordonnées y.
La position de l’objet AB et celle de l’image A’B’ sont respectivement repérées par les abscisses xᴀ de A et xᴀ' de A’.
Les abscisses xᴀ et xᴀ’, la distance focale f’ de la lentille, ne sont pas indépendantes : elles sont reliées par une relation appelée relation de conjugaison.
xA , xA’ et f’ doivent être exprimées avec la même unité de longueur.
La relation de conjugaison permet de déterminer la distance focale de la lentille mince.
La relation de grandissement permet de comparer la taille de l’image et celle de l’objet. Par ailleurs, grâce au théorème de Thalès, on montre que ce rapport est lié aux abscisses qui donnent les positions de l’objet et de l’image (schéma B). Le grandissement 𝜸 est algébrique : il peut être positif ou négatif.
𝜸 n’a pas d’unité.
La position, la taille et le sens de l'image sont les caractéristiques de l'image. Elles sont déterminées graphiquement ou calculées à partir des relations de conjugaison et de grandissement.
Elles dépendent donc de la lentille mince utilisée et des caractéristiques de l'objet.
Activité - Utiliser la relation de conjugaison
Un objet AB est situé à 20,0 cm d’une lentille mince convergente. Son image se forme sur un écran situé à 33,3 cm de la lentille.
Utiliser la relation de conjugaison pour calculer la distance focale f’ de la lentille mince convergente.
Utiliser la relation de conjugaison pour calculer l’abscisse xA’ de l’image A’B’ pour la situation décrite ci-contre.
Utiliser la formule du grandissement
Un objet AB de 2,0 cm de hauteur donne, à travers une lentille mince convergente, une image renversée de 1,0 cm de hauteur.
Calculer le grandissement 𝜸 dans ces conditions.
En utilisant le schéma ci-contre, calculer le grandissement 𝜸 dans ces conditions.
En déduire l’abscisse xᴀ’de l’image A’B’.
Mise au point
Pour que l’image d’un objet se forme sur la rétine d’un œil ou sur le capteur d’un appareil photographique, il est nécessaire de réaliser une mise au point.
Pour réaliser une mise au point, on peut soit modifier la distance focale de la lentille mince convergente, soit modifier la géométrie du montage optique, c’est-à-dire les distances objet – lentille ou lentille – écran.
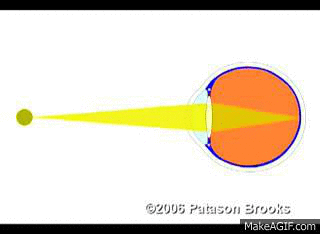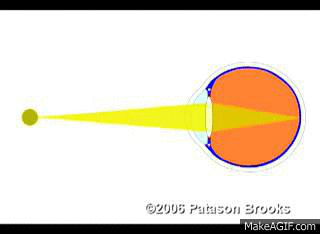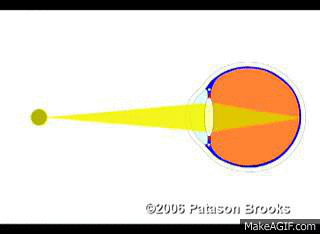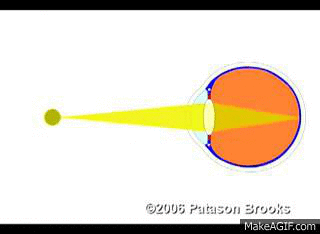

Le lien entre la position de l’objet et les caractéristiques de l’image
Objet AB situé avant le foyer objet F
Caractéristiques de l’image
L’image formée à travers la lentille peut être observée sur un écran.
On dit que l’image est réelle : xA’ > 0.
𝜸 < 0 : l’image est renversée.
Si |𝜸| > 1 : l’image est plus grande que l’objet ;
Si |𝜸| < 1 : l’image est plus petite que l’objet.
Situation
Schématisation
Objet AB situé entre le foyer objet F et le centre optique O
Caractéristiques de l’image
L’image formée à travers la lentille ne peut pas être observée sur un écran.
On dit que l’image est virtuelle : xA’ < 0.
𝜸 > 0 : l’image est droite.
|𝜸| > 1 : l’image est plus grande que l’objet.
Situation
Schématisation
Simulation
Activité
Déterminer les caractéristiques d'une image
À partir de la construction réalisée ci-dessus, déterminer les caractéristiques de l’image :
virtuelle ou réelle ;
plus petite ou plus grande que l’objet ;
renversée ou droite par rapport à l’objet.
Construire l'image donnée par une lentille
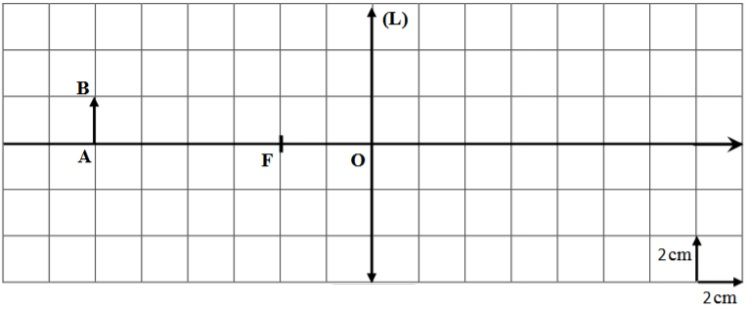
Reproduire le schéma et tracer l’image A’B’ de l’objet AB.
Indiquer les caractéristiques de l’image A’B’ donnée par la lentille mince convergente.
Exercices
Déterminer la position et la taille d’une image par construction graphique
Un appareil photographique numérique est équipé d’un objectif assimilable à une lentille convergente de distance focale 30mm. Une rose de 4 cm de hauteur est située à 12cm de l’appareil. La base de la rose sera prise sur l’axe optique de la lentille constituant l’objectif de l’appareil.
Schématiser la situation, en respectant l’échelle suivante : 1cm sur le schéma représente 2cm horizontalement et verticalement.
Construire l’image de la rose donnée par l’objectif.
Quelles sont les caractéristiques de cette image?
A quelle distance de l’objectif le capteur doit être placé pour que l’image soit nette.
Un oeil très accomodant
L’œil peut être modélisé par une lentille mince convergente et un écran. Lorsque la personne regarde un objet lointain, l’image se forme sur la rétine sans que l’œil ne se fatigue : on dit que l’œil n’accommode pas. Lorsque cette personne regarde un objet proche, son œil accommode pour que l’image se forme sur la rétine. La distance focale de la lentille convergente modélisant son œil est alors modifiée. La distance entre le centre optique de l’œil étudié ici et la rétine est 17 mm.
Dans le cas où l’objet regardé est très éloigné de la lentille, vers quelle valeur le rapport 1/xA tend-il ?
Déduire de la question précédente la distance focale f’de l’œil lorsqu’il regarde au loin.
Indiquer la grandeur modifiée lorsqu’un œil accommode.
L’œil étudié observe un objet situé à 30 cm de lui. Calculer sa distance focale dans ce cas.
Un appareil photographique numérique est équipé d’un objectif assimilable à une lentille convergente de distance focale 30mm. Une rose de 4 cm de hauteur est située à 12cm de l’appareil. La base de la rose sera prise sur l’axe optique de la lentille constituant l’objectif de l’appareil.
Schématiser la situation, en respectant l’échelle suivante : 1cm sur le schéma représente 2cm horizontalement et verticalement.
Construire l’image de la rose donnée par l’objectif.
Quelles sont les caractéristiques de cette image?
A quelle distance de l’objectif le capteur doit être placé pour que l’image soit nette.
Debout !
Commencer par résoudre l’énoncé compact. En cas de difficultés passer à l’énoncé détaillé.
Enoncé compact
Calculer la taille de l’objet dont l’image est projetée au plafond par le radio-réveil.
Enoncé détaillé
En s’appuyant sur la photographie, trouver les caractéristiques de l’image obtenue à travers la lentille mince convergente du radio-réveil.
Utiliser la relation de conjugaison pour déterminer l’abscisse xA de l’affichage de l’heure dans le radio-réveil.
Calculer la taille de l’objet dont l’image est projetée au plafond par le radio-réveil.
Evaluations
QCM - Lentilles minces et convergentes



Laisser un commentaire
Vous devez être Connecté en tant que pour poster un commentaire.
Lewis Orel le 26/09/2020 17:04:52
Impossibilité de faire le Qcm