Lumière : ondes et particules
Ajouter à mes favoris
Notions et compétences attendues
Utiliser l’expression donnant l’énergie d’un photon. Exploiter un diagramme de niveaux d'énergie.
Utiliser une échelle de fréquences ou de longueurs d’onde pour identifier un domaine spectral.
Citer l’ordre de grandeur des fréquences ou des longueurs d’onde des ondes électromagnétiques utilisées dans divers domaines d’application.
Obtenir le spectre d’une source spectrale et l’interpréter à partir du diagramme de niveaux d’énergie des entités qui la constituent.
La lumière et la dualité onde-particule
Modèle ondulatoire
Une onde électromagnétique est caractérisée par sa fréquence ν (en Hz) ou par sa longueur d’onde λ (en m). Comme toutes les ondes, elle transporte de l’énergie mais pas de matière. À la différence des ondes mécaniques, une onde électromagnétique peut se propager dans le vide. La lumière peut être décrite par une onde électromagnétique, on parle de modèle ondulatoire. Dans ce modèle, le rayon lumineux est la direction de propagation de l’énergie électromagnétique transportée par l’onde.
La longueur d’onde λ et la fréquence ν d’une radiation lumineuse sont liées par :
Le spectre des ondes électromagnétiques est divisé en différents domaines qui s’étendent des rayons gamma aux ondes radio.
Les domaines d’application des ondes électromagnétiques sont très variés et dépendent des longueurs d’onde ou des fréquences : santé, communication, astronomie, physique des particules, radioactivité…
Le domaine de la lumière visible s’étend de 400 à 800 nm.

Modèle particulaire
Depuis les travaux d’Albert EINSTEIN publiés en 1905, on sait que la lumière est constituée de particules de masse nulle : les photons. On parle de modèle particulaire de la lumière. Dans ce modèle, le rayon lumineux est la direction de propagation des photons qui se déplacent à la vitesse c.
Une onde électromagnétique, de fréquence ν ou de longueur d’onde λ, peut être décrite par des photons qui transportent chacun un quantum d’énergie E donnée par la relation :

E est l'énergie du photon (en joules) ;
h est la constante de Planck dont une valeur approchée est :
ν la fréquence (en hertz) de l'onde électromagnétique associée au photon considéré ;
λ est la longueur d’onde (en mètre) de l'onde électromagnétique associée au photon considéré ;
c est la vitesse de propagation de la lumière, ou célérité est, dans le vide, et avec trois chiffres significatifs : c = 3,00 x 108 m.s-1.
Activité
La seconde
La seconde est l’une des sept unités de base du Système International (SI). Au XIXe siècle, elle a été définie par rapport à la rotation de la Terre sur elle-même. Quelques décennies plus tard, cette définition n’était plus assez précise. Depuis 1967, la seconde est la durée de 9 192 631 770 périodes de la radiation correspondant à la transition entre deux niveaux d’énergie de l’atome de césium 133. Il en résulte que la fréquence de cette radiation est ν = 9,192 631 770 GHz. Le domaine spectral en fonction de la longueur d’onde des ondes électromagnétiques est donné ci-dessous :

Calculer la longueur d’onde λ de la radiation de fréquence ν correspondant à la transition entre ces deux niveaux d’énergie du césium 133.
Dans quel domaine du spectre des ondes électromagnétiques cette radiation se situe-t-elle ?
Calculer l’énergie du photon associé à cette radiation.
Les horloges au césium affichent la seconde avec une incertitude de l’ordre de 1 x 10^–14 s. Estimer, en microseconde, l’incertitude sur une durée d’une année mesurée avec une horloge au césium en ne tenant compte que de cette source d’erreur.
La lumière et la dualité onde-particule
Quantification de l’énergie des atomes
Les niveaux d’énergie d’un atome sont quantifiés : leur énergie ne peut prendre que certaines valeurs.
Sur un diagramme de niveaux d’énergie :
le niveau d’énergie le plus bas corres-pond à l’état stable de l’atome, appelé état fondamental ;
les autres niveaux correspondent à des états moins stables, appelés états excitésde l’atome.
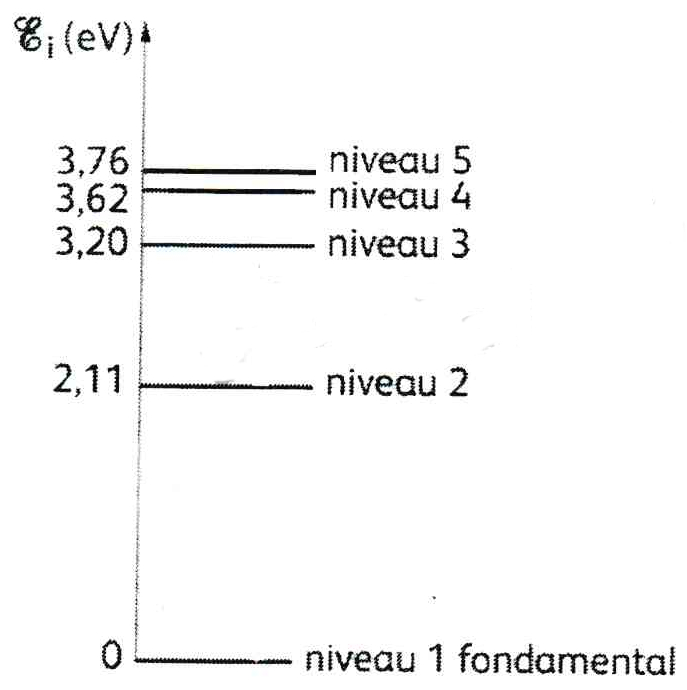
Dans un diagramme de niveaux d’énergie :
l’état de plus haute énergie correspond à la perte d’un électron ; l’atome est dit ionisé. Par convention son énergie notée E∞ est égale à 0 eV ;
les énergies des autres états sont négatives.
Émission et absorption de la lumière par un atome
L’étude des spectres de raies d’émission et d’absorption a permis aux physiciens de comprendre l’interaction lumière-matière.
Au cours d’une transition entre deux états d’énergie Einitial et Efinal, le photon absorbé ou émis par un atome possède une énergie telle que :
Émission de la lumière par un atome
Einitial > Efinal
L’atome perd de l’énergie en émettant un photon.
Sur un diagramme d’énergie, on représente cette transition par une flèche verticale, dirigée vers le bas :
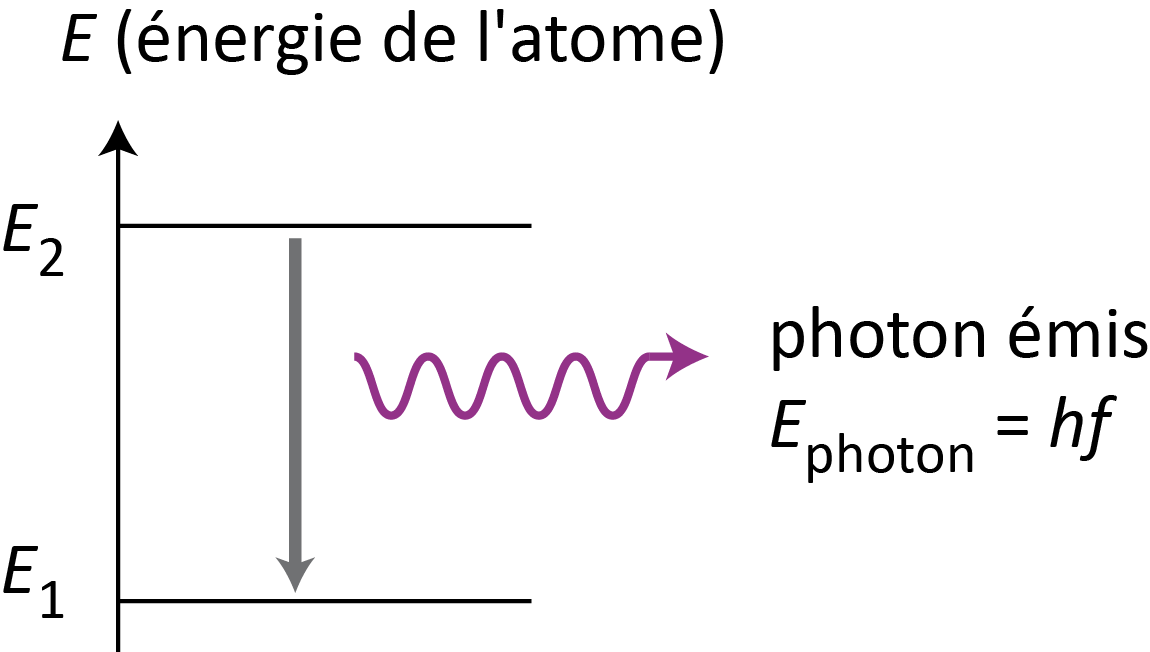 L’énergie libérée est égale à la différence d’énergie entre les deux niveaux : E = |Efinal - Einitial|.
L’énergie libérée est égale à la différence d’énergie entre les deux niveaux : E = |Efinal - Einitial|.
Cette énergie libérée est transportée par un photon dont l’énergie est Ephoton = h x ν.
Il y a donc émission d’une radiation monochromatique. La fréquence ν de cette radiation est telle que : h x ν = |Efinal - Einitial|.
Si cette fréquence appartient au domaine du visible, cette radiation correspond à une raie colorée dans le spectre d’émission de l’atome.
Absorption de lumière par un atome
Einitial < Efinal
L’atome gagne de l’énergie en absorbant un photon.
Sur un diagramme d’énergie, on représente cette transition par une flèche verticale, dirigée vers le haut :
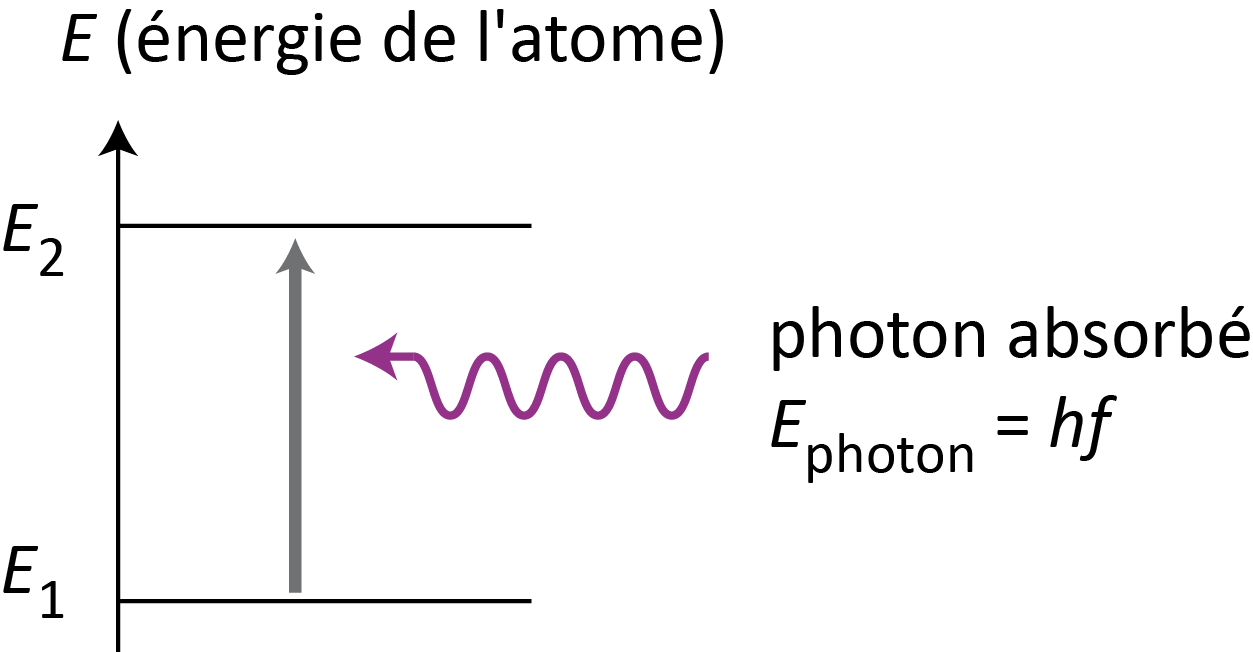 L’énergie absorbée est égale à la différence d’énergie entre les deux niveaux : E = |Efinal - Einitial|.
L’énergie absorbée est égale à la différence d’énergie entre les deux niveaux : E = |Efinal - Einitial|.
Cette énergie apportée est transportée par un photon dont l’énergie est Ephoton = h x ν.
Il y a donc absorption d’une radiation monochromatique. La fréquence ν de cette radiation est telle que : h x ν = |Efinal - Einitial|.
Si cette fréquence appartient au domaine du visible, cette radiation correspond à une raie noire dans le spectre de la lumière blanche.
Chaque entité chimique a son propre diagramme énergétique. Cela explique pourquoi il est possible d’identifier une entité chimique à partir d’un spectre lumineux d’émission ou d’absorption.
Les radiations émises ou absorbées sont caractéristiques d’un atome car elles dépendent des niveaux d’énergie de cet atome.
Activité
Étude de l’atome de lithium
Le diagramme ci-contre représente quelques niveaux d’énergie de l’atome de lithium.
Identifier l’état fondamental et les états excités du lithium.
Déterminer l’énergie que doit transporter un photon pour amener l’atome de lithium de son état fondamental au niveau d’énergie E2.
Exprimer cette énergie en électronvolt (eV) et en joule. 1 eV = 1,60 x 10–19 J
Reproduire le diagramme de niveaux d’énergie de l’atome de lithium et représenter, à l’aide d’une flèche, cette transition.
Lors d’une désexcitation, l’atome de lithium émet une radiation de longueur d’onde λ = 611 nm. Identifier la transition à laquelle cette radiation correspond.
Représenter, à l’aide d’une flèche, cette transition sur le diagramme précédent.
Exercices
Calculer des longueurs d’onde et des fréquences
Dans le tableau ci-dessous, on a indiqué la longueur d’onde λ ou la fréquence ν d’ondes électromagnétiques.Recopier et compléter ce tableau.
| λ | 1,34 µm | 882 nm | |
| ν | 5,0 x 10^13 MHz |
Exploiter une transition énergétique
Le diagramme d'énergie ci-contre est celui de l'atome d'hydrogène.
Quelle énergie doit posséder un photon pour permettre à l'atome de passer du niveau d'énergie E1 au niveau E∞ ?
Représenter cette transition.
Calculer la longueur d'onde correspondante.
Lampe germicide
La lampe germicide est une lampe spécifique qui émet des radiations avec une longueur d’onde de 253,7 nm. Elle est utilisée notamment pour tuer les bactéries, les virus, désinfecter les eaux, l’air dans les hôpitaux.
Déterminer l’ordre de grandeur de la longueur d’onde de la radiation émise.
Ces radiations appartiennent-elles au domaine infrarouge, ultraviolet ou visible ?
Calculer l’énergie des photons émis associés à ces radiations.
Laser femtoseconde
Le laser femtoseconde est utilisé dans la chirurgie de l’œil (myopie). Il délivre des impulsions très brèves, de l’ordre de la femtoseconde, pour éviter des effets thermiques. Un laser de ce type émet des radiations dont la longueur d’onde est λ = 1 µm. Chacune des impulsions transporte une énergie E = 0,1 µJ.
Calculer la fréquence de ces radiations.
Ces radiations appartiennent-elles au domaine infra-rouge, ultraviolet ou visible ?
Calculer l’énergie des photons associés à ces radiations.
En déduire le nombre de photons émis par chaque impulsion.
Lampe à vapeur d’hydrogène
La lumière émise par une lampe à vapeur d’hydrogène permet d’obtenir le spectre suivant sur lequel les longueurs d’onde sont exprimées en nm.

Calculer, en joule puis en électronvolt, l’énergie des photons associés à chacune de ces radiations.
À quelle transition correspond chaque radiation émise par l’atome d’hydrogène ?
Reproduire le diagramme puis y représenter chacune de ces transitions.
Atome de lithium
Le spectre de l’atome de lithium est représenté ci-après :
S’agit-il d’un spectre d’émission ou d’absorption ? Justifier la réponse.
Expliquer l'origine des raies colorées.
Atome de sodium
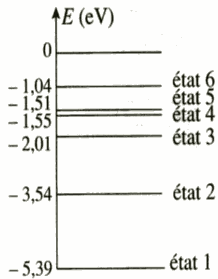
Le diagramme des niveaux d’énergie de l’atome de sodium est donné ci-dessous :
L’atome passe du niveau d’énergie 1 à l’état d’énergie 3. Cette transition a lieu au cours d’une interaction lumière-matière. Les photons mis en jeu sont-ils émis ou absorbés ? Justifier la réponse.
Calculer, en électronvolt (eV), l’énergie d’un photon responsable de cette transition.
Indiquer par une flèche, sur le diagramme des niveaux d’énergie, la transition correspondante.
Exprimer l’énergie d’un photon en fonction de la longueur d’onde λ de la radiation correspondante.
Calculer cette longueur d’onde λ puis donner sa valeur en nm ; à quel domaine de longueur d’onde appartient cette radiation ?
Déterminer également la fréquence du photon.





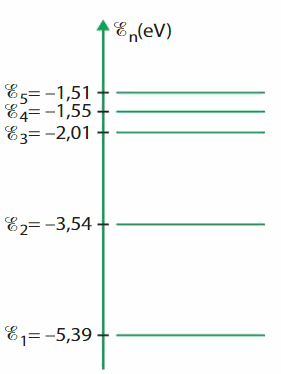
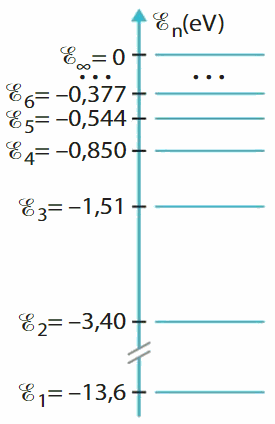

Laisser un commentaire
Vous devez être Connecté en tant que pour poster un commentaire.