Mouvement et modélisation d'une action sur un système
Ajouter à mes favoris
Notions et compétences
Référentiel et relativité du mouvement.
Description du mouvement d'un système par celui d'un point.
Vecteur vitesse d'un point.
Réaliser et exploiter une vidéo ou chronophotographie d'un système en mouvement, et représenter des vecteurs vitesse.
Décrire la variation du vecteur vitesse.
Modélisation d'un action par une force.
Caractéristiques d'une force : force d'interaction gravitationnelle, poids, force exercée par un support et par un fil.
Principe des actions réciproques (troisième loi de Newton)
Relativité du mouvement
Système et référentiels
Avant de commencer toute étude de mouvement, il faut :
identifier l’objet dont on étudie le mouvement. On définit ainsi le système étudié.
indiquer l’objet de référence par rapport auquel on décrit le mouvement. Cet objet de référence est appelé le référentiel. Un référentiel est constitué :
d’un repère d’espace par rapport auquel on repère les positions du système,
d’un repère de temps (horloge) permettant un repérage des dates.
Activité
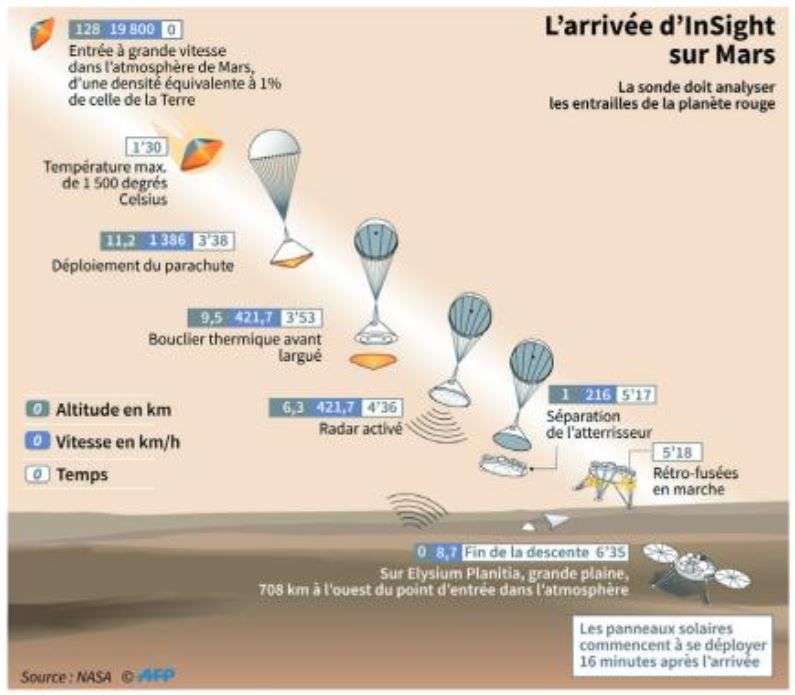
La sonde InSight de la NASA
Après 7 mois de voyage, la sonde InSight de la Nasa a déposé sur la planète Mars le 26 novembre 2018, après 7 minutes d'une délicate descente, SEIS, le sismographe français qui pourra "entendre le coeur de la planète rouge".
Quel est le système dont on étudie le mouvement lors de cette descente ?
Parachute ascentionnel
Identifier 3 systèmes susceptibles d'être en mouvement dans le champ de la photographie
Modélisation d'un système
Pour simplifier l'étude du mouvement, on réduit le système à un point particulier appelée point matériel. La position d'un point matériel est définie par ses coordonnées dans un repère d'espace, graduée à l'aide d'une échelle spatiale adaptée.
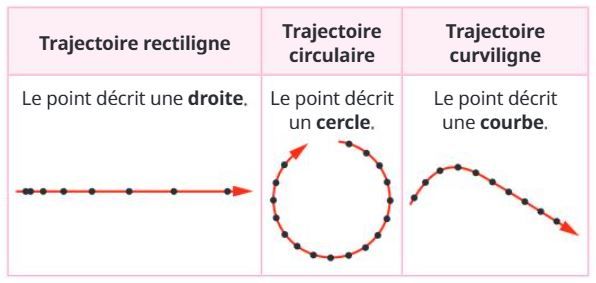
La trajectoire d'un système est l'ensemble des positions successives occupées par le point matériel modélisant le système. Il existe plusieurs types de trajectoire, les plus simples sont rectilignes, circulaires ou curvilignes.

Activité
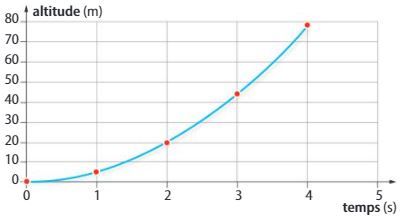
Variation d'altitude
Les bonnes échelles
Quelles sont les échelles spatiale et temporelle les mieux adaptées pour décrire le mouvement d'un ballon de basketball lors d'un lancer franc ?
Dépassement de vitesse
Lorsque deux voitures roulent côte à côte, que peut on dire du mouvement d'une voiture par rapport à l'autre ?
Si le référentiel d'étude est la voiture de droite, quel est dans ce référentiel le mouvement de l'autre voiture ?
Si la voiture "référentiel" freine, quel sera, dans ce référentiel, le mouvement de l'autre voiture ?
Déplacement et vitesse
On définit le vecteur déplacement MM' d'un point lorsque celui-ci se déplace d'une position M à une autre M'.
La vitesse moyenne d'un point peut être représentée par un vecteur v défini par :
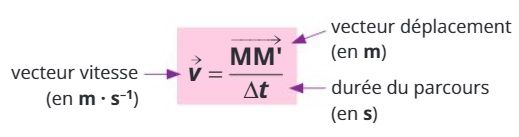
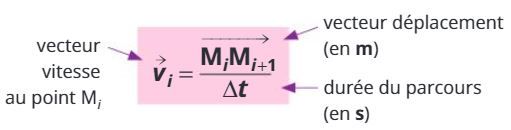
Le vecteur vitesse vi en un point Mi pour un vecteur déplacement MiMi+1 s'écrit :
Ils se représentent ainsi :
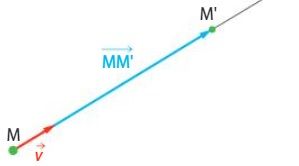
L’évolution de la vitesse du système peut être étudiée sur une image qui représente les positions successives occupées par le système à des intervalles de temps de même durée.
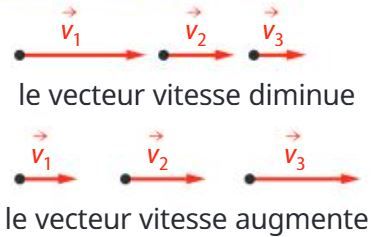
Si le vecteur vitesse ne varie pas, le mouvement est dit rectiligne uniforme.

Si le vecteur vitesse varie, le mouvement est dit rectiligne non uniforme.
Activité
Cycloïde
Les positions occupéres par un point situé à la périphérie de la roue d'un vélo se déplaçant sur un support horizontal, sont représentées toutes les 0,1 s sur le graphique ci-dessous. La courbe est nommée cycloïde.
Donner les coordonnées des positions 1 et 5 dans le repère (O ; x ; y) du graphique.
Quelles sont les coordonnées d'un point de la roue en contact avec le sol ?
Coordonnées manquantes
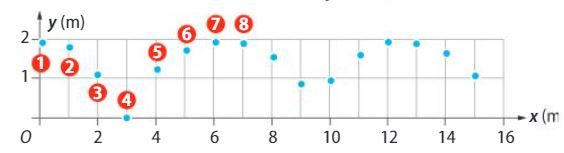
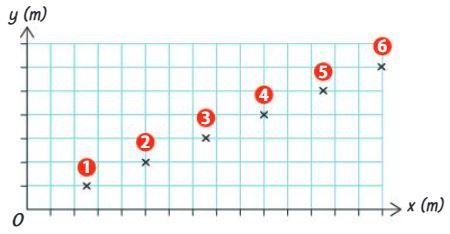
Un élève a représenté les six positions successives occupées par un point en mouvement toutes les 0.10 s dans un repère orthonormée (O ; x ; y). On peut remarquer qu'il manque les valeurs sur les axes et que le tabeau de mesures est incomplet.
Recopier le tableau et le compléter.
Mouvement et vitesse
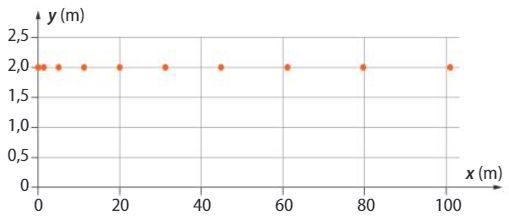
A partir d'un enregistrement vidéo, on obtient toutes les 5 secondes, les coordonnées d'un point en mouvement de la gauche vers la droite.
Déterminer la valeur du vecteur déplacement du point pour l'enregistrement effectué.
En déduire la valeur de la vitesse moyenne.
Repreoduire la trajectoire du point, puis tracer le vecteur vitesse moyenne en utilisant l'échelle suivante : 1 cm pour 1 m.s-1
Modélisation d'une action sur un système
De l'action mécanique à la force
Action mécanique
Les actions mécaniques peuvent avoir différents effets sur le système étudié :
le mettre en mouvement,
modifier sa trajectoire et/ou sa vitesse,
ou encore le déformer.
Action à distance et action de contact
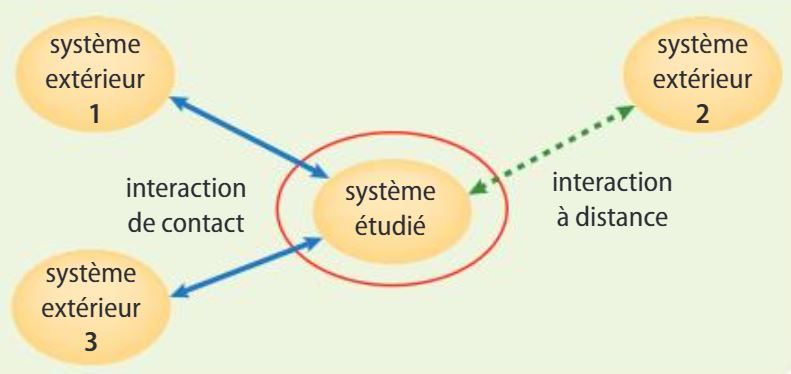
Si les systèmes étudiés et extérieur se touchent, on parle d'action mécanique de contact.Si le système extéieur agit sur le système étudié sans le toucher, on parle d'action mécanique à distance.
Diagramme objets-interactions
Le diagramme objets-interactions permet de dresser schématiquement le bilan des actions mécaniques qui s'exercent sur le système étudié.
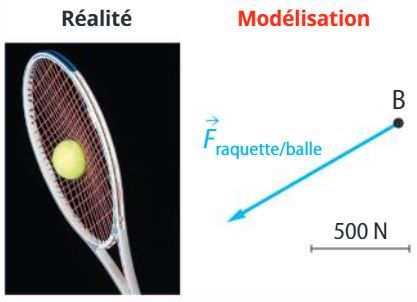
Modélisation d'une action mécanique par une force
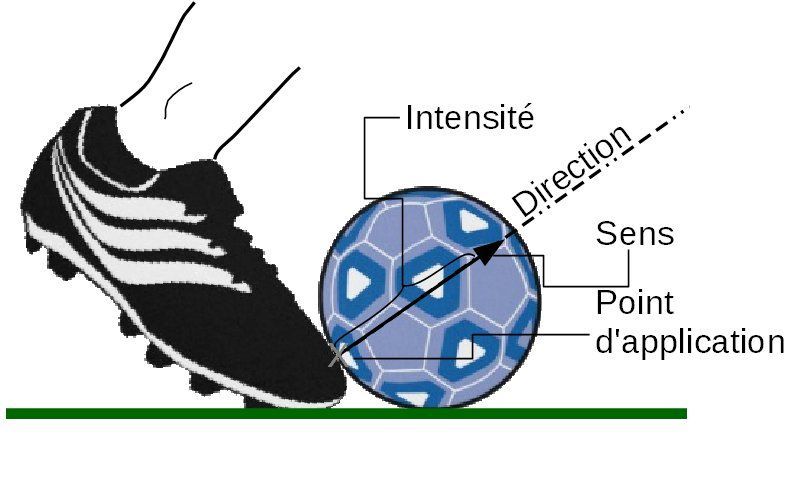
Les caractéristiques d'un vecteur Fsyst.ext/syst.etu sont :
- l'origine, le point représentant le système étudié ;
- la direction, celle de l'action mécanique ;
- le sens, celui de l'action mécanique ;
-la norme (ou longueur) est proportionnelle à la valeur (ou intensité) de la force, exprimée en newton (N).
Exemples de forces
Force d'interaction gravitationnelle
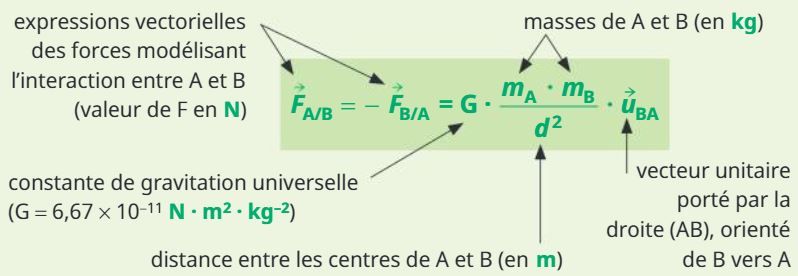
Deux corps A et B dont les masses mA et mB sont régulièrement réparties autour de leur centres distants d'une distance d, exercent l’un sur l’autre des actions attractives de même intensité, de même direction, mais de sens opposés.
Le poids
Le poids d'un système est la force qui modélise l'action à distance de l'astre attracteur à proximité.
L'intensité de pesanteur dépend de la masse de l'astre et de son rayon :
Forces de contact
Forces exercée par un support
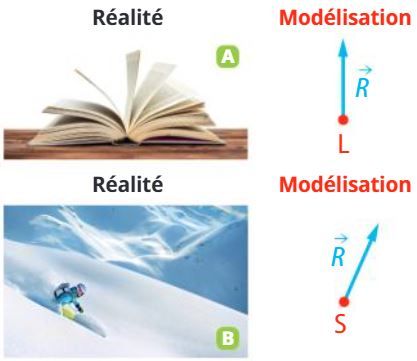
On appelle réaction R du support la force qui modélise l'action du support sur le système d'étude. Les caractéristiques de la réaction R sont :
- la direction qui est perpandiculaire au support ;
- le sens qui est du support vers le système étudié ;
- la norme qui est proportionnelle à la valeur de la réaction R.
Forces de contact
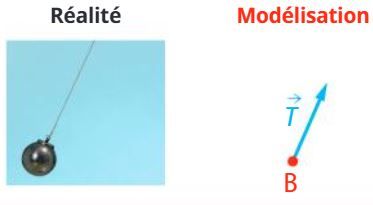
On appelle tension T du fil la force qui modélise l'action du fil sur le système d'tude. Les caractéristiques de la tension T sont :
- la direction qui est celle du fil ;
- le sens qui est du système étudié vers le fil ;
- la norme qui est proportionnelle à la valeur de la tension T.
Activités
Acrobate et tissu aérien
Dessiner le diagramme objets-interactions en prenant l'acrobate comme système d'étude.
Indiquer les actions mécaniques qui s'exercent sur l'acrobate.
Quelles forces modélisent ces actions ?
Lancer de javelot
Voici un dessin d'une athlète lançant un javelot.
On modélise les actions mécaniques suivantes.
Pour chaque modèle :
Indiquer le système d'étude et le système qui agit.
Donner les caractéristiques de la force qui modélise l'action mécanique.
Action de contact ou action à distance
Indiquer si les actions suivantes sont des actions à distance ou des actions de contact.
L'action du pied sur un ballon
L'action de la Terre sur un ballon
L'action de la Terre sur la Lune
L'action du vent sur une planche à voile.
Io et Jupiter
Si la planète Jupiter attire sa lune Io, alors Io attire Jupiter.
Données :
Masse de Io : MI = 8,93 x 10²² kg
Masse de Jupiter : MJ = 1,90 x 10²⁷ kg
Distance Jupiter-Io : d = 4,22 x 10⁵ km
Constante de gravitation universelle : G = 6,67 x 10⁻¹¹ N.m².kg⁻²
Calculer la valeur de la force d'interaction FI/J
Principe des actions réciproques
Troisième loi de Newton
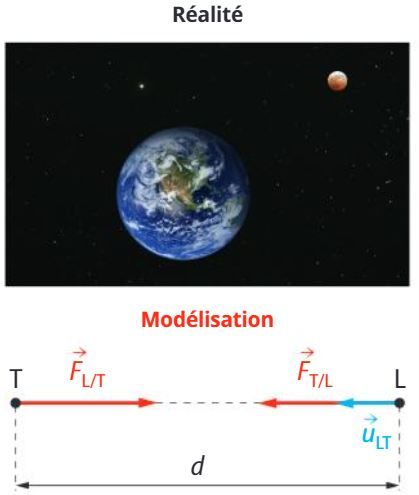
Lorsqu'un système A exerce une action mécanique sur un système B, alors le système B exerce une action mécanique réciproque sur le système A. Ces actions sont modélisées par des forces telles que :
Ces forces ont même direction, même valeur, mais sont de sens opposés.
Activité
Le plongeoir
Lorsqu'une plongeuse saute sur la planche du plongeoir, elle est propulsée vers le haut.
Quelle action la plongeuse exerce-t-elle sur le plongeoir ? Représenter la force modélisant cette action sans soucis d'échelle.
Quelle action propulse la plongeuse ? Représenter la force modélisant cette action sans soucis d'échelle.



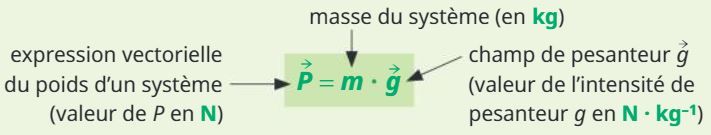
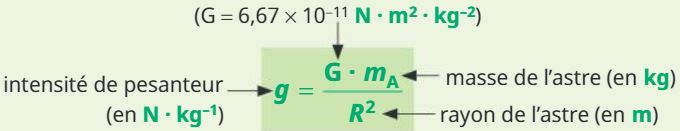
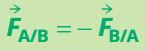
Laisser un commentaire
Vous devez être Connecté en tant que pour poster un commentaire.
Paradigme SASU, Admin le 15/06/2021 18:08:18
Malheureusement non, je fais les corrections en cours directement. Mais tu peux les demander à ton professeur
darka le 30/05/2021 17:00:16
Il y aurait-il les corrections des activités svp ?
Plus particulièrement le lancé de javelot