Deux grandeurs sont proportionnelles lorsque les valeurs de l’une de ces grandeurs s’obtiennent en multipliant (ou en divisant) les valeurs de l’autre grandeur par un même nombre.
Unités et conversions
Ajouter à mes favoris
C’est quoi et à quoi ça sert ?
Unités dans l'antiquité
Dans notre univers, les phénomènes physiques sont très nombreux. Certains tels que les distances ou le temps qui passe, sont essentiels, d'autres plus complexes tels que la gravité terrestre, les pressions ou l'énergie ont été longtemps incompris.
Les premiers phénomènes physiques probablement " étudiés " par l'homme préhistorique furent le temps, les distances (longueurs) et les masses.
Les hommes ont d'abord mesuré les longueurs avec leur corps. Toutes les civilisations ont utilisé des unités en rapport avec la morphologie humaine.
Bien sur si vous essayez de trouvez les dimensions historiques de ces vieilles unités de mesures : pied, empan, palme, paume vous trouverez quantité de valeurs sensiblement différentes. Pendant des millénaires nous n’avons pas été capable d’harmoniser avec des étalons ces mesures, si bien que les étalons variaient toujours de plus ou moins 1 ou 2 %.
Le doigt est une ancienne unité de longueur d’environ 1,85 cm.
Dans l’Antiquité, chez les Égyptiens, les Grecs et les Romains, le doigt était toujours un seizième de pied.
Quelques mesures basées sur la main : (1) le demi-pes manualis ou pied manuel, (2) la main, (3) le palme, (4) l'empan, (5) le doigt, (6) le digit
Pour mesurer le temps, une longueur, une quantité, on se sert d’une unité de mesure.
Exemples :
pour les longueurs on choisit le centimètre, les mètre, le kilomètre …
pour les temps, on utilise la seconde, la minute, l’ heure, le jour, la semaine, le mois, l’année…
pour les masses, on utilise le milligramme, le gramme, le kilogrammes, la tonne …
Pour aller plus loin
Unités : Mode d'emploi
Conversion d'unité
Les multiples et sous multiples d'unités
Si l'unité internationale de longueur est aujourd'hui le mètre, cette longueur est trop petite pour un astronome, comme elle est trop grande pour un bijoutier.
Il est donc nécessaire de pouvoir utiliser des multiples ou des fractions (sous-multiples) de cette unité, mais aussi de pouvoir facilement " naviguer " entre ces nouvelles possibilités.
Il s'est progressivement imposé ce que l'on appelle le système de calcul décimal. Ce système de calcul mathématique consiste à compter jusqu'à 9 (à partir de 0) avant de changer de dizaine.
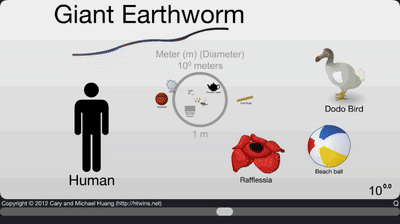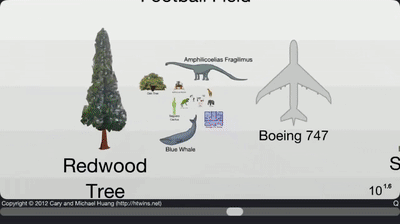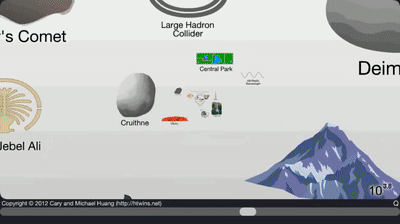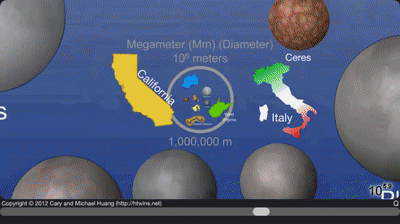
Nous allons maintenant voir comment convertir une valeur exprimée dans une certaine unité de mesure en une valeur exprimée dans une autre unité de mesure. Par exemple, nous allons voir comment on converti des centimètres en mètres.
Périmètre, Aire et Volume
Définitions
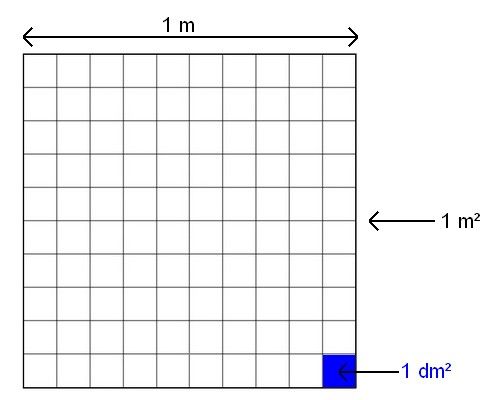
Comme pour les unités de longueur, on peut utiliser des unités d'aire multiples ou sous-multiples du m². Mais il faut faire attention au moment de la conversion. Prenons l'exemple du m² au dm².
On remarque que ce carré contient 10 x 10 carrés de côté 1 dm (ayant donc une aire de 1 dm²). Ainsi, le carré de côté 1 m a une aire de 100 dm². Pour convertir des m² en dm², il faut donc multiplier par 100.
1 m² = 100 dm²
Pour convertir les aires, on peut utiliser un tableau de conversion :
| m2 | dm2 | ||
| 1 | 0 | 0 |
Pour convertir 154,8 cm² en m², on écrit dans le tableau précédent de sorte que :
le chiffre des unités du nombre soit dans la dernière case des cm² ;
chaque case ne contienne qu'un seul chiffre.
| m² | dm² | cm² | mm² | ||||
| 1 | 5 | 4, | 8 | ||||
| 0, | 0 | 1 | 5 | 4 | 8 |
Le périmètre d'une figure est la longueur de son contour.
L'aire d'une figure est la mesure de sa surface intérieure.
Une unité d'aire souvent utilisée est le mètre carré (m²). 1 m² est l'aire d'un carré de côté 1 m.
Temps et durée
Le temps est une donnée particulière, en effet il ne se mesure pas en base 10.
La seconde est l’unité de mesure du temps du système international, de symbole s.
Toutes les autres unités découlent de la seconde :
1 min = 60 s
1 h = 60 min = 3600 s
1 j = 24 h = 1400 min = 86400 s
Conversion en minutes et/ou en secondes
Exprimons 3 h 12 min en minutes, puis en secondes.
3 h = 3 x 60 = 180 min
donc 3 h 12 min = 180 + 12 = 192 min
et 192 min = 192 x 60 = 11 520 s
donc 3 h 12 min = 192 min ou 11 520 s
Conversion en heure décimale
Exprimons 4 h 12 min en heure décimale. Pour cela, il faut convertir les 12 minutes en nombre décimal d’heures.
Méthode 1 : avec un tableau de proportionnalité
| Minutes | 60 | 12 |
| Heures | 1 | x |
x est la valeur recherchée. On applique le produit croisé.
60 * x = 12 * 1
donc x = (12 * 1) : 60 = 0,2
Résultat : 4 h 12 min = 4 h + 0,2 h = 4,2 h
Méthode 2 : avec les fractions
Résultat : 4 h 12 min = 4,2 h
Taux unitaires
Rappel
Un taux fait intervenir la division et sera souvent noté sous la forme d'une fraction .
Un taux unitaire est un taux dont le dénominateur est 1.
2348 vues
0
0
Laisser un commentaire
Vous devez être Connecté en tant que pour poster un commentaire.