Forces, déplacement et énergie
Ajouter à mes favoris
Forces
Action mécanique
Lorsqu'un objet ou système agit sur un autre objet, on parle d'action mécanique.
Une action mécanique exercée sur un système a des effets sur celui-ci, elle peut :
déformer le système ;
elle peut modifier le mouvement du système : l'arrêter ou le mettre en mouvement.
Action de contact
Si les systèmes qui agissent l'un sur l'autre sont en contact, on parle d'action de contact. L'action mécanique de contact est répartie sur toute la surface de contact et s'arrête si il n'y a plus de contact.
Ex : l'action du vent sur une voile, l'action de l'air sur un parachute, d'un marteau sur un clou, etc
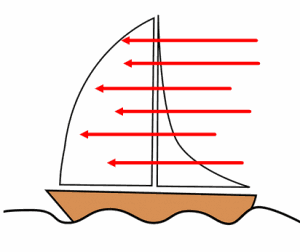
Action à distance
Si les systèmes qui agissennt l'un sur l'autre sont à distance, on parle d'action à distance.
Ex : une bille de fer attirée par un aimant, action de pesanteur
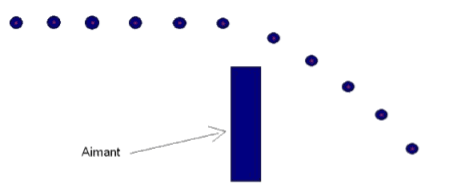
Modélisation
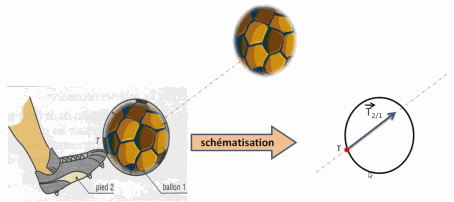
L’action mécanique qui s’exerce sur un système est modélisée par une force.
Une force est schématisée par un vecteur.
Caractéristiques d'une force :
Direction : horizontal, vertical, etc...
Sens : vers le haut, de gauche à droite, de A vers B, etc
Valeur (proportionnelle à la longueur du segment fléché) exprimée en newton (N)
Force d'interaction gravitationnelle
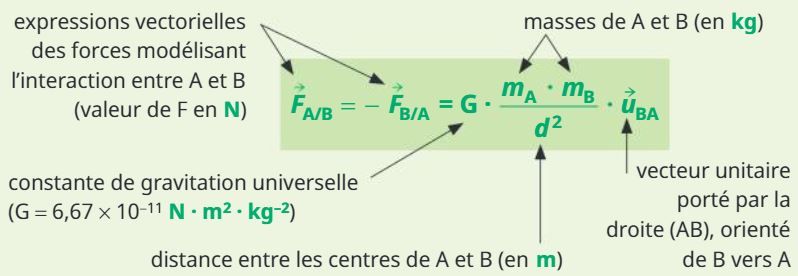
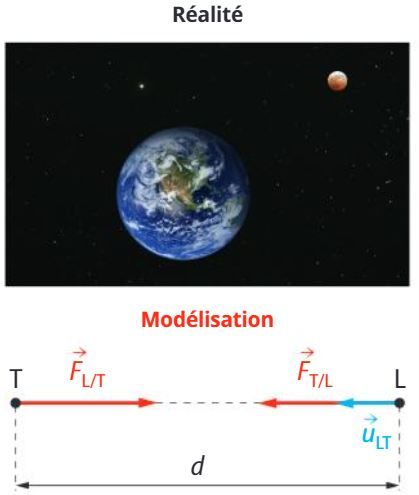
Tous les corps de l’Univers sont en interaction attractive. C’est la gravitation universelle.
Deux corps A et B dont les masses mA et mB sont régulièrement réparties autour de leur centres distants d'une distance d, exercent l’un sur l’autre des actions attractives de même intensité, de même direction, mais de sens opposés.
Le poids
Le poids d'un système est la force qui modélise l'action à distance de l'astre attracteur à proximité.
L'intensité de pesanteur dépend de la masse de l'astre et de son rayon :
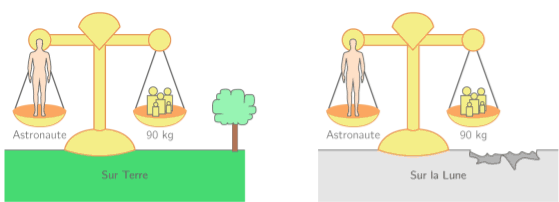
A la surface de chaque astre, règne une intensité de pesanteur g différente. Sur Terre, elle est de 9,8 N.kg-1 et sur la Lune, elle est de 1,6 N.kg-1.
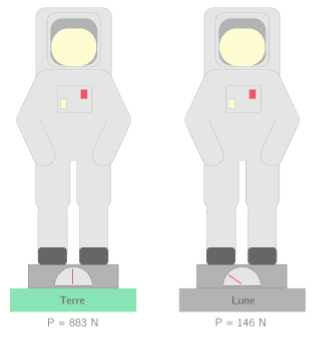
La valeur du poids d’un corps est environ six fois plus faible sur la Lune que sur la Terre..
Activités
Comparaison du poids d’un objet sur la Terre et sur la Lune
Quels sont les 3 caractéristiques du vecteur poids d’un objet de masse m ?
Calculer l’intensité de l’attraction terrestre g en un point de sa surface
Calculer l’intensité de l’attraction lunaire gL en un point de sa surface
Calculer le poids d’un cosmonaute de masse m = 80 kg , sur la Lune et sur la Terre.
Données : masse de la Lune : mL = 7,34 x 10^22 kg ; rayon de la Lune : RL = 1740 km.
Données : masse de la terre : mT = 5,97 x 10^24 kg ; Rayon de la Terre : RT = 6,37 x 10^6 m
Concours d'haltérophilie
On organise un concours d'haltérophilie entre les élèves de la classe.
Quel masse maximale pensez vous pouvoir lever sur Terre ?
Calculer le poids que représente cette masse sur Terre.
Sur quelle planète du système solaire :
Vous pourrez lever une masse plus importante que sur Terre? Quelle masse maximale pourrez vous lever sur cette planète ?
Vous ne pourrez pas lever une masse plus importante que sur Terre? Quelle masse maximale pourrez vous lever sur cette planète ?
Mouvement
Evolution de la vitesse
L’évolution de la vitesse du système peut être étudiée sur une image qui représente les positions successives occupées par le système à des intervalles de temps de même durée.
Principe d'inertie
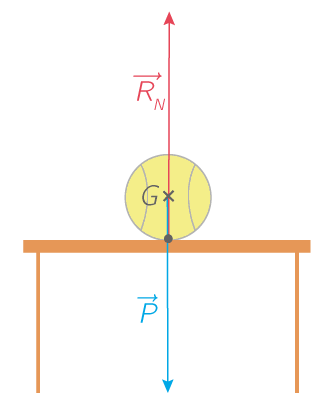
Un corps est immobile ou en mouvement rectiligne uniforme si et seulement si les forces qui s’exercent sur lui se compensent. Il en serait de même si le corps n’était soumis à aucune force.

Principe fondamental de la dynamique
La somme (résultante) des forces extérieurs exercées sur un objet est toujours égale au produit de la masse de cet objet par son accélération. De plus, l'accélération produite et la force résultante ont la même orientation :
Avec :
les forces extérieures exercées sur l'objet, en N ;
la masse de l'objet, en kg ;
l'accélération de l'objet en m/s² ;
Si la résultante des forces extérieures est nulle alors, en accord avec le principe d'inertie :
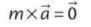
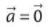

Activités
Le bucheron et le tronc
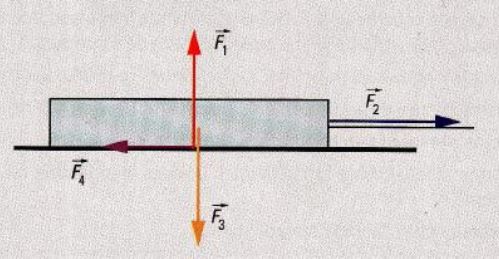
Un bûcheron a abattu un arbre gigantesque et en a coupé toutes les branches. Il le rapporte à la scierie en l'attachant à l'arrière de son tracteur à l'aide d'un câble. On a représenté ci dessous les forces exercées sur le tronc à un certain moment du voyage.
Identifier chacune des forces exercées sur le tronc.
Au moment représenté ici, d'après le principe d'inertie, le tronc est-il en mouvement rectiligne uniforme ?
Sortie de route
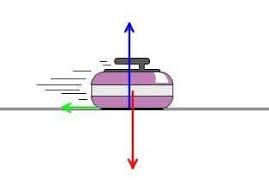
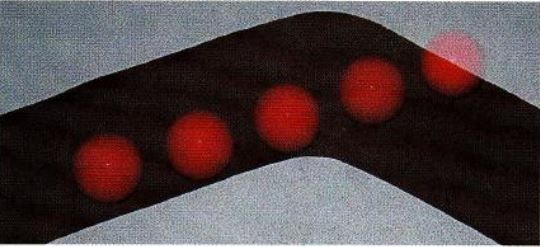
Quelle est la nature du mouvement de la boule ?
A quelles forces est elle soumise ?
Expliquer pourquoi il est impossible de faire suivre ce trajet courbe par la boule ?
Une voiture aborde un virage. Que va t il se passer si les forces qui agissent sur cette voiture se compensent ?
Caractéristiques d’une force
Faire l’inventaire des forces s’appliquant à la masse puis déterminer les caractéristiques de ces forces (on négligera les frottements).
Force de frottement de contact solide-solide
Lorsqu'il n'y a pas de traction, le solide subit deux forces, son poids et la réaction du support. Les forces se compensent : le solide est immobile.
Lorsqu'il y a adhérence (pas de déplacement), le solide est soumis à une force de traction F, mais il reste immobile car il est aussi soumis à des forces de frottement f. Tant que f < μs x N, avec μs le coefficient d'adhérence, le solide adhère au sol.
f < μs x N
Lorsqu'il y a glissement, le solide est soumis à une force de traction F et se déplace. La somme des forces est non nulle avec f = μ x N, avec μ le coefficient de glissement, tel que μ < μs.
f = μ x N
Coefficient de glissement
Soit un objet de masse m = 50 kg glissant sur le sol en subissant les forces indiquées sur la figure ci-dessous.
Quelles sont les forces s'exerçant sur l'objet ?
Quelle est la valeur du poids ?
En déduire la valeur de la réaction du support.
Quelle est la valeur de la force de frottement sachant que le coefficient de glissement μ vaut 0,50 ?
Plan incliné
Pour déterminer le coefficient de frottement statique μs aluminium-acier, on place un morceau d'aluminium sur un plan en acier dont on peut mesurer l'inclinaison.
On augmente l'angle entre le plan incliné et l'horizontale. On mesure la valeur de l'angle pour laquelle le solide S commence à glisser : a = 20°.
Faire le bilan des forces au moment où le solide décroche.
Quelle est la relation entre la force de frottement f, la réaction du support N au plan incliné et le coefficient de frottement statique μs ?
Montrer que tan(a) = f/N.
En déduire la valeur du coefficient de frottement statique μs.
Energie
Notion
L'énergie d'un système exprime sa capacité à modifier l'état d'autres systèmes avec lesquels il est en interaction. Son unité est le joule (J).
L'énergie est une grandeur qui peut prendre plusieurs formes. Sa caractéristique est qu'elle ne peut être ni créée ni détruite. Ainsi, l'énergie d'un système isolé se conserve.
Energie potentielle de pesanteur
L'énergie potentielle de pesanteur Ep d'un système de masse m est l'énergie qu'il possède du fait de son altitude z par rapport à la référence des énergies potentielles de pesanteur :
Energie cinétique
L'énergie cinétique Ec d'un système de masse m animé d'un mouvement de translation est l'énergie qu'il possède du fait de sa vitesse de valeur v :
Energie transférée par le travail d'une force
Une force peut transférer ou absorber de l'énergie à un système en mouvement.
Le travail d'une force représente l'énergie développée par la force lors du déplacement du système. Il peut être moteur ou résistant.
Pour un solide en translation, le travail d’une force F dont le point d’application se déplace de A vers B est égal à :

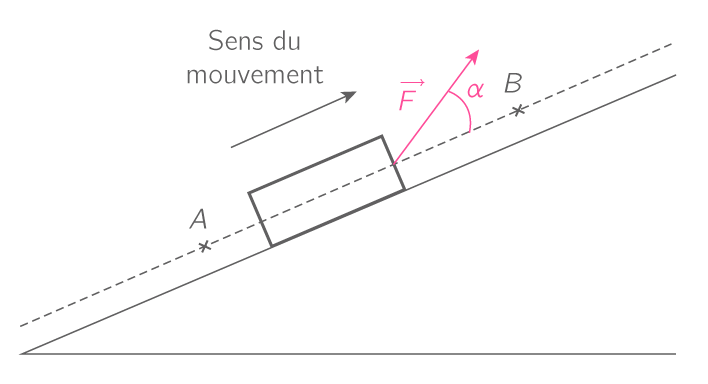
Si le travail est positif, on dit qu'il est moteur : cela signifie que la force en question favorise le déplacement du système.
Si le travail est négatif, on dit qu'il est résistant : cela signifie que la force en question gêne le déplacement du système.
Energie mécanique
L'énergie mécanique d'un système Em s'exprime comme la somme de son énergie cinétique Ec et de son énergie potentielle Ep :
Em = Ec + Ep
Activités
Travail d'une force
Calculer le travail d’une force WAB(F) lorsque :
F = 15 N ; ℓ = 5,0 m ; α = 0° ;
F = 2,5 kN ; ℓ = 25 cm ; α =180° ;
F = 98 mN ; ℓ= 348 mm ; α =90°.
Théorèmes des énergies cinétiques et mécaniques
Théorèmes des énergies cinétiques et mécaniques
Les théorèmes de l'énergie cinétique et mécanique permettent de relier les variations d'énergie du système au travail des forces qu'il subit.
Théorème de l'énergie cinétique
Le théorème de l'énergie cinétique permet de relier la variation de vitesse du système au travail des forces extérieures qu'il subit. Son application directe permet de déterminer la valeur d'une grandeur inconnue du mouvement.
Dans un référentiel galiléen, la variation de l'énergie cinétique d'un système de masse m se déplaçant d'un point A à un point B, est égale à la somme des travaux des forces extérieures qu'il subit :
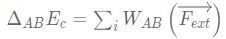
Activités
Parachutiste en chute libre
Un parachutiste de 90 kg tombe en chute libre. On supposera qu’il n’est soumis qu’à son poids (on néglige les frottements de l’air).
Au début de la chute du parachutiste, à un point A, sa vitesse est nulle. Quelle est son énergie cinétique EA?
Après une hauteur de chute h jusqu’à un point B, sa vitesse est de 35 km.h–1. Que vaut alors son énergie cinétique EB?
Appliquer le théorème de l’énergie cinétique pour déterminer le travail du poids WAB(P) lors de cette chute.
Le travail du poids est-il moteur ou résistant lors de ce déplacement ?
En déduire la hauteur h=AB de la chute.
Freinage d’urgence d’un camion
Un camion de 33 tonnes roulant à 90 km.h–1 se met à freiner en urgence et met 200 m à s’immobiliser. On supposera que seule la force de freinage travaille lors de ce déplacement.
Pourquoi le travail du poids est-il nul lors de ce déplacement ?
Pourquoi le travail de la réaction de la route sur la remorque est-il nul lors de ce déplacement ?
Calculer l’énergie cinétique EA du camion au début du freinage.
Calculer son énergie cinétique EB à l’arrêt.
Appliquer le théorème de l’énergie cinétique pour déterminer le travail de la force de freinage WAB(F) lors de ce freinage.
Lors de ce déplacement, le travail de la force de freinage est-il moteur ou résistant ?
En déduire l’intensité de la force de freinage.
Freinage d’une voiture
Une voiture de 800 kg roule à 50 km/h et se met à freiner avec une force freinage f d'intensité 4 000N. On souhaite déterminer la distance mis par le véhicule pour s'arrêter totalement.
Faire le bilan des forces s'appliquant sur la voiture.
Calculer le travail de ces forces.
Calculer l'énergie cinétique de la voiture au début et à la fin du freinage.
Appliquer le théorème de l'énergie cinétique afin de déterminer la distance mise par le véhicule pour s'arrêter.
Théorème de l'énergie mécanique
Le théorème de l'énergie mécanique permet de relier la somme des énergies d'un système au travail des forces qu'il subit. Son application directe permet de déterminer la valeur d'une grandeur inconnue du mouvement.
Au cours d'un mouvement d'un système entre un point A et un point B, la variation d'énergie mécanique d'un système est égale au travail des forces non conservatives

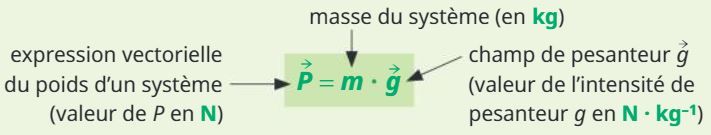
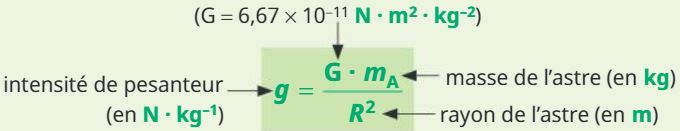

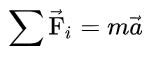
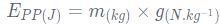
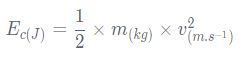
Laisser un commentaire
Vous devez être Connecté en tant que pour poster un commentaire.